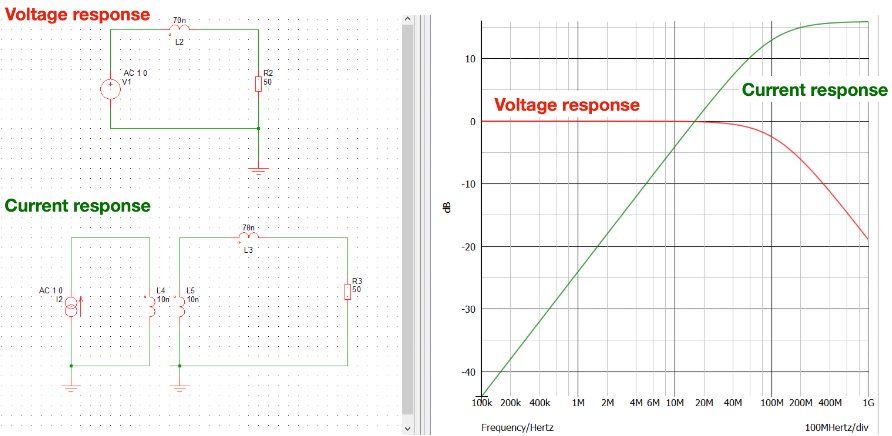
by Dr. Min Zhang, the EMC Consultant
Here is a classic question; – where should we put the filter with regard to the noise source? Shall we place the filter close to the noise source or away from it? The answer is; – if you can, you should always place the filter in a quiet environment, i.e. away from the noise source.
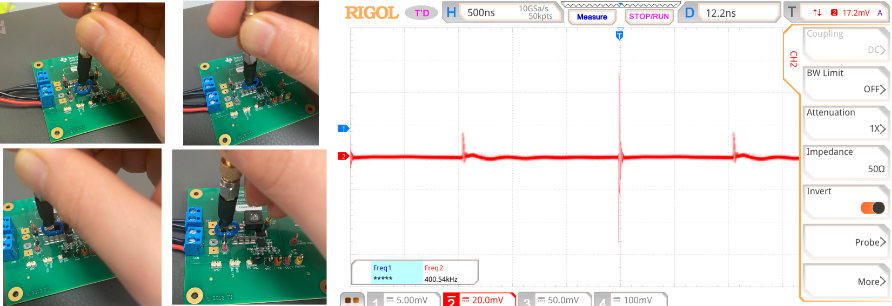
Here we should not get confused with what we say about ‘solving EMI problems at the noise source’. We all know that the best approach to solving EMI problems is to suppress the noise source. Without understanding the principles, engineers often put an EMI filter close to the noise side, such as a SMPS on a PCB, or a line filter close to a motor drive circuit. This creates problems because the strong leakage field of the noise source will couple strongly with the passive components of a filter. As a result, a carefully designed filter, which is supposed to give 60-80 dB attenuation according to the simulation/calculation, often ends up having only 10-20 dB insertion loss. This is particularly true when the frequency increases.
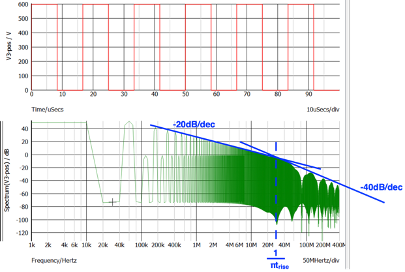
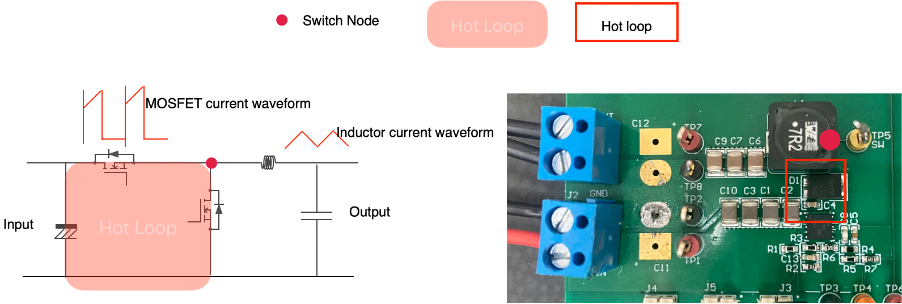
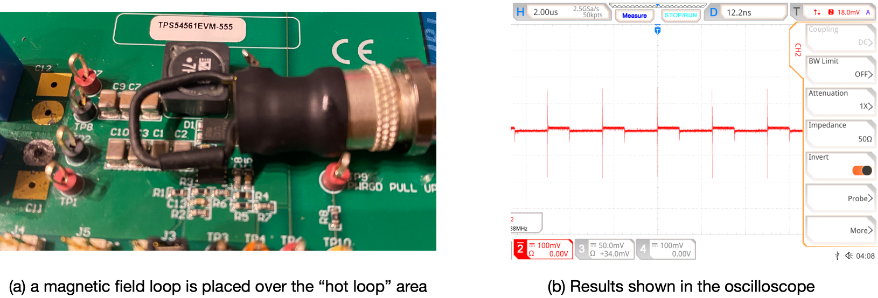
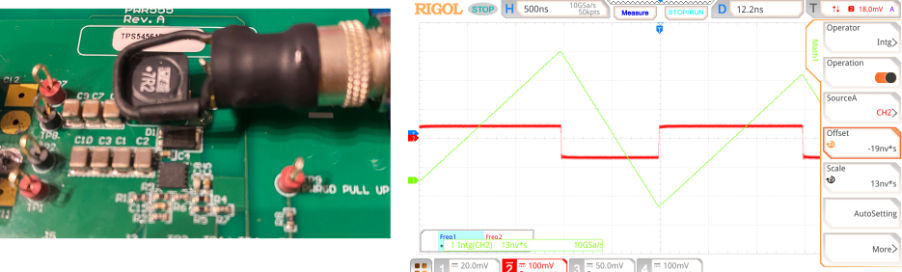
The circuit shown in Figure 1 is given to demonstrate the point. The input stage of a typical buck converter using in integrated switching IC is shown. On the input side, the filter stage is separated from the input capacitors by including the red dashed line. Note that there can never be a strict separation line between the filter and the input capacitors as the input capacitors also provide a low impedance path to noise, so they work nicely with the filter. But here the two are separated to make the point.
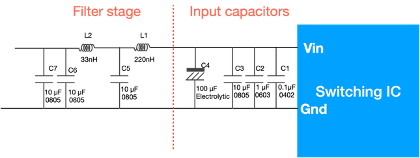
The input capacitors are part of the SMPS design. Therefore, one will need to design the capacitors to make sure there is always enough energy delivered in the most efficient way whenever the switch is turned on. This is often achieved by the following:
- Populate the input supply rail with several decoupling capacitor sizes (0402, 0603, 0805, etc) so that energy is available over a wide frequency spectrum.
- The decoupling capacitors should be connected as close as possible to the Vin pin.
- Locate the smallest size capacitor (in this case C1, 0402) first to the Vin pin.
- The electrolytic capacitor C4 serves as the main energy storage device, but it also provides damping of the system due to its relatively larger ESR.
- If the electrolytic capacitor has a metal housing, such as aluminium, due to the larger size of the electrolytic capacitor, the metal housing also serves as a shield to block some of the electric field created by the SMPS.
The filter stage is designed as a multi-stage filter which consists of two inductors and a few ceramic capacitors. The red line shown in Figure 1 indicates that there must be a distance between the filter and the input capacitors. This is to avoid field coupling and make the input filter stage more effective. On a PCB level, this is often achieved through the following steps:
- Put the input filter away from the noise source, if the noise source is a SMPS and it is located on one side of the PCB, the safe side of a filter should be on the opposite side of a PCB.
- If the filter stage has to be on the same side of the SMPS, a physically long distance shall be kept. The distance depends on the strength of the leakage field of the SMPS. For instance, if the switch node of the SMPS is kept quiet by a shield, then the distance between the filter and SMPS can be shortened.
- The connection between the filter stage and the input capacitors should always be a high impedance path such as an inductor (L1 shown in Figure 1).
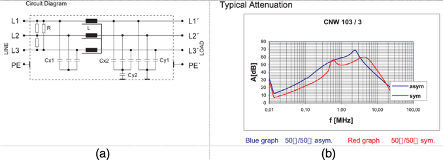
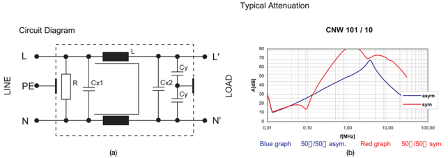
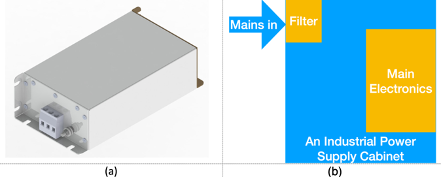
The same principle applies to much larger systems such as an industrial motor drive system or power supply. For instance, a line filter used for an industrial motor drive application such as the one shown in Figure 2 (a) is always much more effective if it is placed near the mains entry point of the cabinet, i.e. to keep the mains wiring and the line filter far away from other wiring and harnessing inside the cabinet. Again, the reason is to avoid close field coupling between the noise source and the filter component.
Training
If you want to learn more about EMC and become an expert in troubleshooting EMI problems. Why not attend our video training course? Priced from $199, you can get 10 hour lessons. Check https://mach1design-shop.fedevel.education/itemDetail.html?itemtype=course&dbid=1644339825702&instrid=us-east-2_4pKkzzNo1:fe56227a-47c8-4ea8-ba6f-2930d01d7db8